Apply Affine Transform From Homogeneous Matrix and Resample#

Synopsis#

Given one homogeneous matrix (here a 3x3 matrix), apply the corresponding transform to a given image and resample using a WindowedSincInterpolateImageFunction.

Results#

Code#

C++#

#include "itkImageFileReader.h"
#include "itkImageFileWriter.h"
#include "itkAffineTransform.h"
#include "itkResampleImageFilter.h"
#include "itkWindowedSincInterpolateImageFunction.h"

int
main(int argc, char * argv[])
{
  if (argc != 4)
  {
    std::cerr << "Usage: " << std::endl;
    std::cerr << argv[0];
    std::cerr << " <InputFileName> <OutputFileName> <DefaultPixelValue>";
    std::cerr << std::endl;
    return EXIT_FAILURE;
  }

  constexpr unsigned int Dimension = 2;
  using ScalarType = double;

  const char * inputFileName = argv[1];
  const char * outputFileName = argv[2];
  const auto   defaultValue = static_cast<ScalarType>(std::stod(argv[3]));

  using MatrixType = itk::Matrix<ScalarType, Dimension + 1, Dimension + 1>;
  MatrixType matrix;
  matrix[0][0] = std::cos(0.05);
  matrix[0][1] = std::sin(0.05);
  matrix[0][2] = 0.;

  matrix[1][0] = -matrix[0][1];
  matrix[1][1] = matrix[0][0];
  matrix[1][2] = 0.;

  matrix[2][0] = -10.;
  matrix[2][1] = -20.;
  matrix[2][2] = 1.;

  using PixelType = unsigned char;
  using ImageType = itk::Image<PixelType, Dimension>;

  const auto input = itk::ReadImage<ImageType>(inputFileName);

  const ImageType::SizeType & size = input->GetLargestPossibleRegion().GetSize();

  using ResampleImageFilterType = itk::ResampleImageFilter<ImageType, ImageType>;
  auto resample = ResampleImageFilterType::New();
  resample->SetInput(input);
  resample->SetReferenceImage(input);
  resample->UseReferenceImageOn();
  resample->SetSize(size);
  resample->SetDefaultPixelValue(defaultValue);

  constexpr unsigned int Radius = 3;
  using InterpolatorType = itk::WindowedSincInterpolateImageFunction<ImageType, Radius>;
  auto interpolator = InterpolatorType::New();

  resample->SetInterpolator(interpolator);

  using TransformType = itk::AffineTransform<ScalarType, Dimension>;
  auto transform = TransformType::New();

  // get transform parameters from MatrixType
  TransformType::ParametersType parameters(Dimension * Dimension + Dimension);
  for (unsigned int i = 0; i < Dimension; ++i)
  {
    for (unsigned int j = 0; j < Dimension; ++j)
    {
      parameters[i * Dimension + j] = matrix[i][j];
    }
  }
  for (unsigned int i = 0; i < Dimension; ++i)
  {
    parameters[i + Dimension * Dimension] = matrix[i][Dimension];
  }
  transform->SetParameters(parameters);

  resample->SetTransform(transform);

  try
  {
    itk::WriteImage(resample->GetOutput(), outputFileName);
  }
  catch (const itk::ExceptionObject & error)
  {
    std::cerr << "Error: " << error << std::endl;
    return EXIT_FAILURE;
  }

  return EXIT_SUCCESS;
}

Classes demonstrated#

template<typename TParametersValueType = double, unsigned int NDimensions = 3> class AffineTransform : public itk::MatrixOffsetTransformBase<TParametersValueType, NDimensions, NDimensions>

Affine transformation of a vector space (e.g. space coordinates)

This class allows the definition and manipulation of affine transformations of an n-dimensional affine space (and its associated vector space) onto itself. One common use is to define and manipulate Euclidean coordinate transformations in two and three dimensions, but other uses are possible as well.

An affine transformation is defined mathematically as a linear transformation plus a constant offset. If A is a constant n x n matrix and b is a constant n-vector, then y = Ax+b defines an affine transformation from the n-vector x to the n-vector y.

The difference between two points is a vector and transforms linearly, using the matrix only. That is, (y1-y2) = A*(x1-x2).

The AffineTransform class determines whether to transform an object as a point or a vector by examining its type. An object of type Point transforms as a point; an object of type Vector transforms as a vector.

One common use of affine transformations is to define coordinate conversions in two- and three-dimensional space. In this application, x is a two- or three-dimensional vector containing the “source” coordinates of a point, y is a vector containing the “target” coordinates, the matrix A defines the scaling and rotation of the coordinate systems from the source to the target, and b defines the translation of the origin from the source to the target. More generally, A can also define anisotropic scaling and shearing transformations. Any good textbook on computer graphics will discuss coordinate transformations in more detail. Several of the methods in this class are designed for this purpose and use the language appropriate to coordinate conversions.

Any two affine transformations may be composed and the result is another affine transformation. However, the order is important. Given two affine transformations T1 and T2, we will say that “precomposing T1 with T2” yields the transformation which applies T1 to the source, and then applies T2 to that result to obtain the target. Conversely, we will say that “postcomposing T1 with T2” yields the transformation which applies T2 to the source, and then applies T1 to that result to obtain the target. (Whether T1 or T2 comes first lexicographically depends on whether you choose to write mappings from right-to-left or vice versa; we avoid the whole problem by referring to the order of application rather than the textual order.)

There are two template parameters for this class:

TParametersValueType The type to be used for scalar numeric values. Either float or double.

NDimensions The number of dimensions of the vector space.

This class provides several methods for setting the matrix and vector defining the transform. To support the registration framework, the transform parameters can also be set as an Array<double> of size (NDimension + 1) * NDimension using method SetParameters(). The first (NDimension x NDimension) parameters defines the matrix in row-major order (where the column index varies the fastest). The last NDimension parameters defines the translation in each dimensions.

This class also supports the specification of a center of rotation (center) and a translation that is applied with respect to that centered rotation. By default the center of rotation is set to the origin.

Subclassed by itk::AzimuthElevationToCartesianTransform< TParametersValueType, NDimensions >, itk::CenteredAffineTransform< TParametersValueType, NDimensions >, itk::ScalableAffineTransform< TParametersValueType, NDimensions >

See itk::AffineTransform for additional documentation.

template<typename TInputImage, unsigned int VRadius, typename TWindowFunction = Function::HammingWindowFunction<VRadius>, class TBoundaryCondition = ZeroFluxNeumannBoundaryCondition<TInputImage, TInputImage>, class TCoordRep = double> class WindowedSincInterpolateImageFunction : public itk::InterpolateImageFunction<TInputImage, TCoordRep>

Use the windowed sinc function to interpolate.

This function is intended to provide an interpolation function that has minimum aliasing artifacts, in contrast to linear interpolation. According to sampling theory, the infinite-support sinc filter, whose Fourier transform is the box filter, is optimal for resampling a function. In practice, the infinite support sinc filter is approximated using a limited support ‘windowed’ sinc filter.

Author: Paul A. Yushkevich
THEORY

Use this filter the way you would use any ImageInterpolationFunction, so for instance, you can plug it into the

ResampleImageFilter class. In order to initialize the filter you must choose several template parameters.

This function is based on the following publication:

Erik H. W. Meijering, Wiro J. Niessen, Josien P. W. Pluim, Max A. Viergever: Quantitative Comparison of Sinc-Approximating Kernels for Medical Image Interpolation. MICCAI 1999, pp. 210-217

In this work, several ‘windows’ are estimated. In two dimensions, the interpolation at a position (x,y) is given by the following expression:

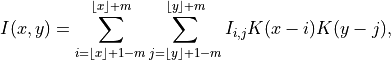
$I(x,y) = \sum_{i = \lfloor x \rfloor + 1 - m}^{\lfloor x \rfloor + m} \sum_{j = \lfloor y \rfloor + 1 - m}^{\lfloor y \rfloor + m} I_{i,j} K(x-i) K(y-j),$

where m is the ‘radius’ of the window, (3,4 are reasonable numbers), and K(t) is the kernel function, composed of the sinc function and one of several possible window functions:

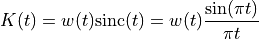
$K(t) = w(t) \textrm{sinc}(t) = w(t) \frac{\sin(\pi t)}{\pi t}$

Several window functions are provided here in the itk::Function namespace. The conclusions of the referenced paper suggest to use the Welch, Cosine, Kaiser, and Lanczos windows for m = 4,5. These are based on error in rotating medical images w.r.t. the linear interpolation method. In some cases the results achieve a 20-fold improvement in accuracy.

USING THIS FILTER

There are a few improvements that an enthusiastic ITK developer could make to this filter. One issue is with the way that the kernel is applied. The computational expense comes from two sources: computing the kernel weights K(t) and multiplying the pixels in the window by the kernel weights. The first is done more or less efficiently in

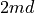$2 m d$ operations (where d is the dimensionality of the image). The second can be done better. Presently, each pixel 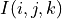$I(i,j,k)$ is multiplied by the weights 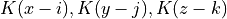$K(x-i), K(y-j), K(z-k)$ and added to the running total. This results in 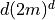$d (2m)^d$ multiplication operations. However, by keeping intermediate sums, it would be possible to do the operation in 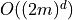$O ( (2m)^d )$ operations. This would require some creative coding. In addition, in the case when one of the coordinates is integer, the computation could be reduced by an order of magnitude.

: The first (TInputImage) is the image type, that’s standard.
: The second (VRadius) is the radius of the kernel, i.e., the 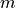$m$ from the formula above.
: The third (TWindowFunction) is the window function object, which you can choose from about five different functions defined in this header. The default is the Hamming window, which is commonly used but not optimal according to the cited paper.
: The fourth (TBoundaryCondition) is the boundary condition class used to determine the values of pixels that fall off the image boundary. This class has the same meaning here as in the NeighborhoodItetator classes.
: The fifth (TCoordRep) is again standard for interpolating functions, and should be float or double.
CAVEATS

See: LinearInterpolateImageFunction ResampleImageFilter
See: Function::HammingWindowFunction
See: Function::CosineWindowFunction
See: Function::WelchWindowFunction
See: Function::LanczosWindowFunction
See: Function::BlackmanWindowFunction

See itk::WindowedSincInterpolateImageFunction for additional documentation.

template<typename TInputImage, typename TOutputImage, typename TInterpolatorPrecisionType = double, typename TTransformPrecisionType = TInterpolatorPrecisionType> class ResampleImageFilter : public itk::ImageToImageFilter<TInputImage, TOutputImage>

Resample an image via a coordinate transform.

ResampleImageFilter resamples an existing image through some coordinate transform, interpolating via some image function. The class is templated over the types of the input and output images.

Note that the choice of interpolator function can be important. This function is set via SetInterpolator(). The default is LinearInterpolateImageFunction<InputImageType, TInterpolatorPrecisionType>, which is reasonable for ordinary medical images. However, some synthetic images have pixels drawn from a finite prescribed set. An example would be a mask indicating the segmentation of a brain into a small number of tissue types. For such an image, one does not want to interpolate between different pixel values, and so NearestNeighborInterpolateImageFunction< InputImageType, TCoordRep > would be a better choice.

If an sample is taken from outside the image domain, the default behavior is to use a default pixel value. If different behavior is desired, an extrapolator function can be set with SetExtrapolator().

Output information (spacing, size and direction) for the output image should be set. This information has the normal defaults of unit spacing, zero origin and identity direction. Optionally, the output information can be obtained from a reference image. If the reference image is provided and UseReferenceImage is On, then the spacing, origin and direction of the reference image will be used.

Since this filter produces an image which is a different size than its input, it needs to override several of the methods defined in ProcessObject in order to properly manage the pipeline execution model. In particular, this filter overrides ProcessObject::GenerateInputRequestedRegion() and ProcessObject::GenerateOutputInformation().

This filter is implemented as a multithreaded filter. It provides a DynamicThreadedGenerateData() method for its implementation.

Warning

For multithreading, the TransformPoint method of the user-designated coordinate transform must be threadsafe.

ITK Sphinx Examples: