Mutual Information Affine#
Synopsis#
Global registration by maximizing the mutual information and using an affine transform.
Results#

Fixed#
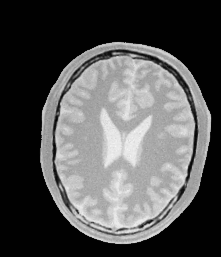
Moving#
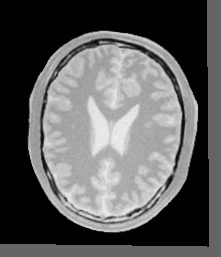
Output#
Output:
Optimizer stop condition: GradientDescentOptimizer: Maximum number of iterations (200) exceeded.
Final Parameters: [1.0028069041777101, -0.009647107048100798, -0.010717116855425006, 1.0029040091646872, 13.26279335943067, 12.226979744206531]
Result =
Iterations = 200
Metric value = 0.000971698
Numb. Samples = 567
Jupyter Notebook#
Code#
C++#
#include "itkImageRegistrationMethod.h"
#include "itkAffineTransform.h"
#include "itkMutualInformationImageToImageMetric.h"
#include "itkGradientDescentOptimizer.h"
#include "itkNormalizeImageFilter.h"
#include "itkDiscreteGaussianImageFilter.h"
#include "itkResampleImageFilter.h"
#include "itkCastImageFilter.h"
#include "itkCheckerBoardImageFilter.h"
#include "itkEllipseSpatialObject.h"
#include "itkSpatialObjectToImageFilter.h"
#include "itkImageFileWriter.h"
#include "itkImageFileReader.h"
constexpr unsigned int Dimension = 2;
using PixelType = unsigned char;
using ImageType = itk::Image<PixelType, Dimension>;
int
main(int argc, char * argv[])
{
if (argc < 4)
{
std::cout << "Usage: " << argv[0] << " imageFile1 imageFile2 outputFile" << std::endl;
return EXIT_FAILURE;
}
ImageType::Pointer fixedImage = itk::ReadImage<ImageType>(argv[1]);
ImageType::Pointer movingImage = itk::ReadImage<ImageType>(argv[2]);
// We use floats internally
using InternalImageType = itk::Image<float, Dimension>;
// Normalize the images
using NormalizeFilterType = itk::NormalizeImageFilter<ImageType, InternalImageType>;
auto fixedNormalizer = NormalizeFilterType::New();
auto movingNormalizer = NormalizeFilterType::New();
fixedNormalizer->SetInput(fixedImage);
movingNormalizer->SetInput(movingImage);
// Smooth the normalized images
using GaussianFilterType = itk::DiscreteGaussianImageFilter<InternalImageType, InternalImageType>;
auto fixedSmoother = GaussianFilterType::New();
auto movingSmoother = GaussianFilterType::New();
fixedSmoother->SetVariance(2.0);
movingSmoother->SetVariance(2.0);
fixedSmoother->SetInput(fixedNormalizer->GetOutput());
movingSmoother->SetInput(movingNormalizer->GetOutput());
using TransformType = itk::AffineTransform<double, Dimension>;
using OptimizerType = itk::GradientDescentOptimizer;
using InterpolatorType = itk::LinearInterpolateImageFunction<InternalImageType, double>;
using RegistrationType = itk::ImageRegistrationMethod<InternalImageType, InternalImageType>;
using MetricType = itk::MutualInformationImageToImageMetric<InternalImageType, InternalImageType>;
auto transform = TransformType::New();
auto optimizer = OptimizerType::New();
auto interpolator = InterpolatorType::New();
auto registration = RegistrationType::New();
registration->SetOptimizer(optimizer);
registration->SetTransform(transform);
registration->SetInterpolator(interpolator);
auto metric = MetricType::New();
registration->SetMetric(metric);
// The metric requires a number of parameters to be selected, including
// the standard deviation of the Gaussian kernel for the fixed image
// density estimate, the standard deviation of the kernel for the moving
// image density and the number of samples use to compute the densities
// and entropy values. Details on the concepts behind the computation of
// the metric can be found in Section
// \ref{sec:MutualInformationMetric}. Experience has
// shown that a kernel standard deviation of $0.4$ works well for images
// which have been normalized to a mean of zero and unit variance. We
// will follow this empirical rule in this example.
metric->SetFixedImageStandardDeviation(5.0);
metric->SetMovingImageStandardDeviation(5.0);
registration->SetFixedImage(fixedSmoother->GetOutput());
registration->SetMovingImage(movingSmoother->GetOutput());
fixedNormalizer->Update();
ImageType::RegionType fixedImageRegion = fixedNormalizer->GetOutput()->GetBufferedRegion();
registration->SetFixedImageRegion(fixedImageRegion);
using ParametersType = RegistrationType::ParametersType;
ParametersType initialParameters(transform->GetNumberOfParameters());
// rotation matrix (identity)
initialParameters[0] = 1.0; // R(0,0)
initialParameters[1] = 0.0; // R(0,1)
initialParameters[2] = 0.0; // R(1,0)
initialParameters[3] = 1.0; // R(1,1)
// translation vector
initialParameters[4] = 0.0;
initialParameters[5] = 0.0;
registration->SetInitialTransformParameters(initialParameters);
// Software Guide : BeginLatex
//
// We should now define the number of spatial samples to be considered in
// the metric computation. Note that we were forced to postpone this setting
// until we had done the preprocessing of the images because the number of
// samples is usually defined as a fraction of the total number of pixels in
// the fixed image.
//
// The number of spatial samples can usually be as low as $1\%$ of the total
// number of pixels in the fixed image. Increasing the number of samples
// improves the smoothness of the metric from one iteration to another and
// therefore helps when this metric is used in conjunction with optimizers
// that rely of the continuity of the metric values. The trade-off, of
// course, is that a larger number of samples result in longer computation
// times per every evaluation of the metric.
//
// It has been demonstrated empirically that the number of samples is not a
// critical parameter for the registration process. When you start fine
// tuning your own registration process, you should start using high values
// of number of samples, for example in the range of $20\%$ to $50\%$ of the
// number of pixels in the fixed image. Once you have succeeded to register
// your images you can then reduce the number of samples progressively until
// you find a good compromise on the time it takes to compute one evaluation
// of the Metric. Note that it is not useful to have very fast evaluations
// of the Metric if the noise in their values results in more iterations
// being required by the optimizer to converge. You must then study the
// behavior of the metric values as the iterations progress.
const unsigned int numberOfPixels = fixedImageRegion.GetNumberOfPixels();
const auto numberOfSamples = static_cast<unsigned int>(numberOfPixels * 0.01);
metric->SetNumberOfSpatialSamples(numberOfSamples);
// For consistent results when regression testing.
metric->ReinitializeSeed(121212);
// Note that large values of the learning rate will make the optimizer
// unstable. Small values, on the other hand, may result in the optimizer
// needing too many iterations in order to walk to the extrema of the cost
// function. The easy way of fine tuning this parameter is to start with
// small values, probably in the range of $\{5.0,10.0\}$. Once the other
// registration parameters have been tuned for producing convergence, you
// may want to revisit the learning rate and start increasing its value until
// you observe that the optimization becomes unstable. The ideal value for
// this parameter is the one that results in a minimum number of iterations
// while still keeping a stable path on the parametric space of the
// optimization. Keep in mind that this parameter is a multiplicative factor
// applied on the gradient of the Metric. Therefore, its effect on the
// optimizer step length is proportional to the Metric values themselves.
// Metrics with large values will require you to use smaller values for the
// learning rate in order to maintain a similar optimizer behavior.
optimizer->SetLearningRate(1.0);
// Note that the only stop condition for the v3 GradientDescentOptimizer class
// is that the maximum number of iterations is reached.
// For the option to exit early on convergence use GradientDescentOptimizerv4
// with an accompanying v4 metric class.
optimizer->SetNumberOfIterations(200);
optimizer->MaximizeOn(); // We want to maximize mutual information (the default of the optimizer is to minimize)
auto scales = optimizer->GetScales();
// Let optimizer take
// large steps along translation parameters,
// moderate steps along rotational parameters,
// and small steps along scale parameters
scales.SetSize(6);
scales.SetElement(0, 100);
scales.SetElement(1, 0.5);
scales.SetElement(2, 0.5);
scales.SetElement(3, 100);
scales.SetElement(4, 0.0001);
scales.SetElement(5, 0.0001);
optimizer->SetScales(scales);
try
{
registration->Update();
std::cout << "Optimizer stop condition: " << registration->GetOptimizer()->GetStopConditionDescription()
<< std::endl;
}
catch (const itk::ExceptionObject & err)
{
std::cout << "ExceptionObject caught !" << std::endl;
std::cout << err << std::endl;
return EXIT_FAILURE;
}
ParametersType finalParameters = registration->GetLastTransformParameters();
std::cout << "Final Parameters: " << finalParameters << std::endl;
unsigned int numberOfIterations = optimizer->GetCurrentIteration();
double bestValue = optimizer->GetValue();
// Print out results
std::cout << std::endl;
std::cout << "Result = " << std::endl;
std::cout << " Iterations = " << numberOfIterations << std::endl;
std::cout << " Metric value = " << bestValue << std::endl;
std::cout << " Numb. Samples = " << numberOfSamples << std::endl;
using ResampleFilterType = itk::ResampleImageFilter<ImageType, ImageType>;
auto finalTransform = TransformType::New();
finalTransform->SetParameters(finalParameters);
finalTransform->SetFixedParameters(transform->GetFixedParameters());
auto resample = ResampleFilterType::New();
resample->SetTransform(finalTransform);
resample->SetInput(movingImage);
resample->SetSize(fixedImage->GetLargestPossibleRegion().GetSize());
resample->SetOutputOrigin(fixedImage->GetOrigin());
resample->SetOutputSpacing(fixedImage->GetSpacing());
resample->SetOutputDirection(fixedImage->GetDirection());
resample->SetDefaultPixelValue(100);
itk::WriteImage(resample->GetOutput(), argv[3]);
return EXIT_SUCCESS;
}
Classes demonstrated#
-
template<typename TParametersValueType = double, unsigned int NDimensions = 3>
class AffineTransform : public itk::MatrixOffsetTransformBase<TParametersValueType, NDimensions, NDimensions> Affine transformation of a vector space (e.g. space coordinates)
This class allows the definition and manipulation of affine transformations of an n-dimensional affine space (and its associated vector space) onto itself. One common use is to define and manipulate Euclidean coordinate transformations in two and three dimensions, but other uses are possible as well.
An affine transformation is defined mathematically as a linear transformation plus a constant offset. If A is a constant n x n matrix and b is a constant n-vector, then y = Ax+b defines an affine transformation from the n-vector x to the n-vector y.
The difference between two points is a vector and transforms linearly, using the matrix only. That is, (y1-y2) = A*(x1-x2).
The AffineTransform class determines whether to transform an object as a point or a vector by examining its type. An object of type Point transforms as a point; an object of type Vector transforms as a vector.
One common use of affine transformations is to define coordinate conversions in two- and three-dimensional space. In this application, x is a two- or three-dimensional vector containing the “source” coordinates of a point, y is a vector containing the “target” coordinates, the matrix A defines the scaling and rotation of the coordinate systems from the source to the target, and b defines the translation of the origin from the source to the target. More generally, A can also define anisotropic scaling and shearing transformations. Any good textbook on computer graphics will discuss coordinate transformations in more detail. Several of the methods in this class are designed for this purpose and use the language appropriate to coordinate conversions.
Any two affine transformations may be composed and the result is another affine transformation. However, the order is important. Given two affine transformations T1 and T2, we will say that “precomposing T1 with T2” yields the transformation which applies T1 to the source, and then applies T2 to that result to obtain the target. Conversely, we will say that “postcomposing T1 with T2” yields the transformation which applies T2 to the source, and then applies T1 to that result to obtain the target. (Whether T1 or T2 comes first lexicographically depends on whether you choose to write mappings from right-to-left or vice versa; we avoid the whole problem by referring to the order of application rather than the textual order.)
There are two template parameters for this class:
TParametersValueType The type to be used for scalar numeric values. Either float or double.
NDimensions The number of dimensions of the vector space.
This class provides several methods for setting the matrix and vector defining the transform. To support the registration framework, the transform parameters can also be set as an Array<double> of size (NDimension + 1) * NDimension using method SetParameters(). The first (NDimension x NDimension) parameters defines the matrix in row-major order (where the column index varies the fastest). The last NDimension parameters defines the translation in each dimensions.
This class also supports the specification of a center of rotation (center) and a translation that is applied with respect to that centered rotation. By default the center of rotation is set to the origin.
Subclassed by itk::AzimuthElevationToCartesianTransform< TParametersValueType, NDimensions >, itk::CenteredAffineTransform< TParametersValueType, NDimensions >, itk::ScalableAffineTransform< TParametersValueType, NDimensions >
-
template<typename TFixedImage, typename TMovingImage>
class MutualInformationImageToImageMetric : public itk::ImageToImageMetric<TFixedImage, TMovingImage> Computes the mutual information between two images to be registered.
MutualInformationImageToImageMetric computes the mutual information between a fixed and moving image to be registered.
This class is templated over the FixedImage type and the MovingImage type.
The fixed and moving images are set via methods SetFixedImage() and SetMovingImage(). This metric makes use of user specified Transform and Interpolator. The Transform is used to map points from the fixed image to the moving image domain. The Interpolator is used to evaluate the image intensity at user specified geometric points in the moving image. The Transform and Interpolator are set via methods SetTransform() and SetInterpolator().
The method
GetValue() computes of the mutual information while method GetValueAndDerivative() computes both the mutual information and its derivatives with respect to the transform parameters.- Warning
This metric assumes that the moving image has already been connected to the interpolator outside of this class.
The calculations are based on the method of Viola and Wells where the probability density distributions are estimated using Parzen windows.
By default a Gaussian kernel is used in the density estimation. Other option include Cauchy and spline-based. A user can specify the kernel passing in a pointer a KernelFunctionBase using the SetKernelFunction() method.
Mutual information is estimated using two sample sets: one to calculate the singular and joint pdf’s and one to calculate the entropy integral. By default 50 samples points are used in each set. Other values can be set via the SetNumberOfSpatialSamples() method.
Quality of the density estimate depends on the choice of the kernel’s standard deviation. Optimal choice will depend on the images. It is can be shown that around the optimal variance, the mutual information estimate is relatively insensitive to small changes of the standard deviation. In our experiments, we have found that a standard deviation of 0.4 works well for images normalized to have a mean of zero and standard deviation of 1.0. The variance can be set via methods SetFixedImageStandardDeviation() and SetMovingImageStandardDeviation().
Implementaton of this class is based on: Viola, P. and Wells III, W. (1997). “Alignment by Maximization of Mutual Information” International Journal of Computer Vision, 24(2):137-154
- See
KernelFunctionBase
- See
GaussianKernelFunction
- ITK Sphinx Examples:
-
class GradientDescentOptimizer : public itk::SingleValuedNonLinearOptimizer
Implement a gradient descent optimizer.
GradientDescentOptimizer implements a simple gradient descent optimizer. At each iteration the current position is updated according to

The learning rate is a fixed scalar defined via SetLearningRate(). The optimizer steps through a user defined number of iterations; no convergence checking is done.
Additionally, user can scale each component,
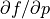 , by setting a scaling vector using method SetScale().
, by setting a scaling vector using method SetScale().- See
RegularStepGradientDescentOptimizer
Subclassed by itk::QuaternionRigidTransformGradientDescentOptimizer
