Download this example

Scale an Image

Synopsis

Scale an image.

Results

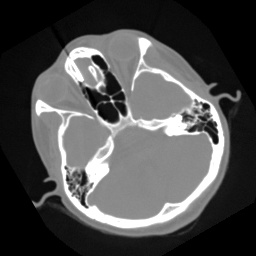
Input Image

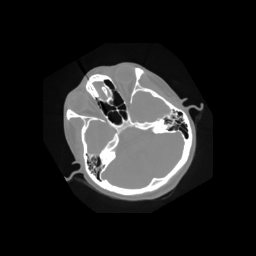
Output Image

Code

C++

#include "itkImage.h"
#include "itkScaleTransform.h"
#include "itkImageFileReader.h"
#include "itkImageFileWriter.h"
#include "itkResampleImageFilter.h"

int
main(int argc, char * argv[])
{
  if (argc < 3)
  {
    std::cerr << "Usage: " << argv[0] << " inputFile outputFile" << std::endl;
  }

  using PixelType = unsigned char;
  constexpr unsigned int ImageDimension = 2;
  using ImageType = itk::Image<PixelType, ImageDimension>;
  auto image = itk::ReadImage<ImageType>(argv[1]);

  using MetricValueType = double;
  using TransformType = itk::ScaleTransform<MetricValueType, 2>;
  auto                      scaleTransform = TransformType::New();
  itk::FixedArray<float, 2> scale;
  scale[0] = 1.5; // newWidth/oldWidth
  scale[1] = 1.5;
  scaleTransform->SetScale(scale);

  itk::Point<float, 2> center;
  center[0] = image->GetLargestPossibleRegion().GetSize()[0] / 2;
  center[1] = image->GetLargestPossibleRegion().GetSize()[1] / 2;

  scaleTransform->SetCenter(center);

  using ResampleImageFilterType = itk::ResampleImageFilter<ImageType, ImageType, MetricValueType>;
  auto resampleFilter = ResampleImageFilterType::New();
  resampleFilter->SetTransform(scaleTransform);
  resampleFilter->SetInput(image);
  resampleFilter->SetSize(image->GetLargestPossibleRegion().GetSize());
  resampleFilter->Update();

  itk::WriteImage(resampleFilter->GetOutput(), argv[2]);

  return EXIT_SUCCESS;
}

Python …

import sys

import itk

if len(sys.argv) < 3:
    raise Exception(f"Usage: {sys.argv[0]} inputFile outputFile")

image = itk.imread(sys.argv[1], itk.UC)

image_dimension = image.GetImageDimension()

transform = itk.ScaleTransform[itk.D, 2].New(
    scale=[1.5] * image_dimension, center=[x / 2 for x in itk.size(image)]
)

scaled_image = itk.resample_image_filter(
    image, transform=transform, size=itk.size(image)
)

itk.imwrite(scaled_image, sys.argv[2])

Classes demonstrated

template<typename TParametersValueType = float, unsigned int NDimensions = 3>
class ScaleTransform : public itk::MatrixOffsetTransformBase<TParametersValueType, NDimensions, NDimensions>

Scale transformation of a vector space (e.g. space coordinates)

The same functionality could be obtained by using the Affine transform, but with a large difference in performance since the affine transform will use a matrix multiplication using a diagonal matrix.

ITK Sphinx Examples:

• All ITK Sphinx Examples

• Scale An Image

Subclassed by itk::ScaleLogarithmicTransform< TParametersValueType, NDimensions >

See itk::ScaleTransform for additional documentation.