Filter Image in Fourier Domain#
Synopsis#
Filter an Image in the Fourier Domain One of the most common image processing operations performed in the Fourier Domain is the masking of the spectrum in order to modulate a range of spatial frequencies from the input image. This operation is typically performed by taking the input image, computing its Fourier transform using a FFT filter, masking the resulting image in the Fourier domain with a mask, and finally taking the result of the masking and computing its inverse Fourier transform.
Results#
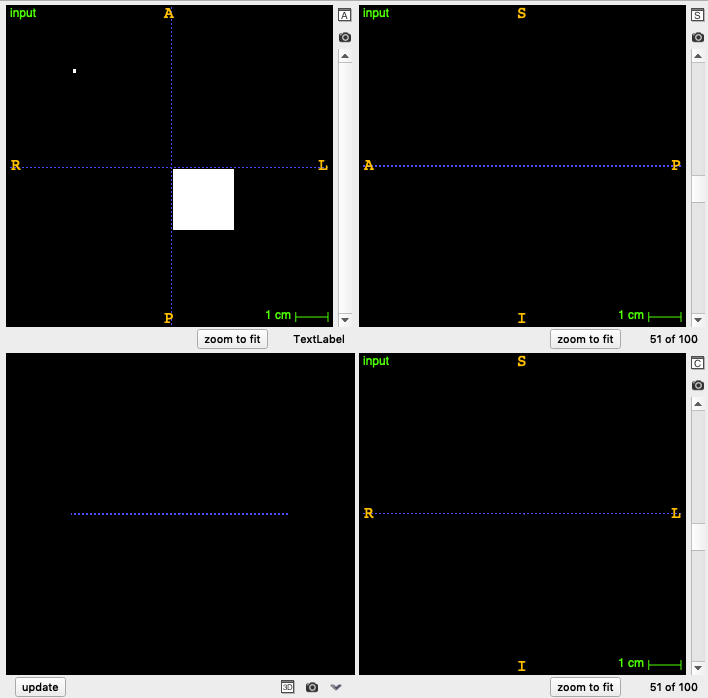
Input image#
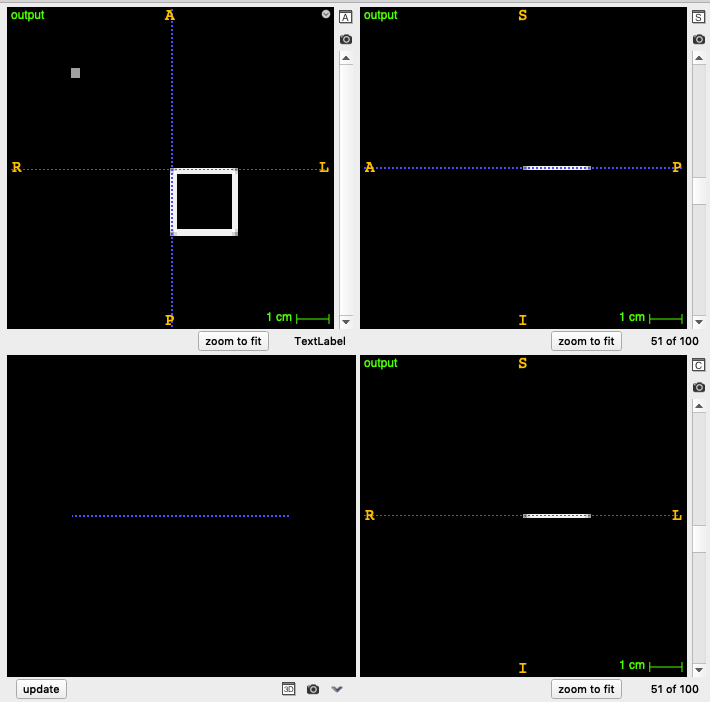
Output image#
Code#
C++#
#include "itkImageFileReader.h"
#include "itkImageFileWriter.h"
#include "itkWrapPadImageFilter.h"
#include "itkForwardFFTImageFilter.h"
#include "itkGaussianImageSource.h"
#include "itkFFTShiftImageFilter.h"
#include "itkMultiplyImageFilter.h"
#include "itkInverseFFTImageFilter.h"
int
main(int argc, char * argv[])
{
if (argc < 3)
{
std::cerr << "Usage: " << std::endl;
std::cerr << argv[0];
std::cerr << " <InputFileName> <OutputFileName>";
std::cerr << " [Sigma]";
std::cerr << std::endl;
return EXIT_FAILURE;
}
const char * inputFileName = argv[1];
const char * outputFileName = argv[2];
double sigmaValue = 0.5;
if (argc > 3)
{
sigmaValue = std::stod(argv[3]);
}
constexpr unsigned int Dimension = 3;
using PixelType = float;
using RealImageType = itk::Image<PixelType, Dimension>;
const auto input = itk::ReadImage<RealImageType>(inputFileName);
// Some FFT filter implementations, like VNL's, need the image size to be a
// multiple of small prime numbers.
using PadFilterType = itk::WrapPadImageFilter<RealImageType, RealImageType>;
auto padFilter = PadFilterType::New();
padFilter->SetInput(input);
PadFilterType::SizeType padding;
// Input size is [48, 62, 42]. Pad to [48, 64, 48].
padding[0] = 0;
padding[1] = 2;
padding[2] = 6;
padFilter->SetPadUpperBound(padding);
using ForwardFFTFilterType = itk::ForwardFFTImageFilter<RealImageType>;
using ComplexImageType = ForwardFFTFilterType::OutputImageType;
auto forwardFFTFilter = ForwardFFTFilterType::New();
forwardFFTFilter->SetInput(padFilter->GetOutput());
try
{
forwardFFTFilter->UpdateOutputInformation();
}
catch (const itk::ExceptionObject & error)
{
std::cerr << "Error: " << error << std::endl;
return EXIT_FAILURE;
}
// A Gaussian is used here to create a low-pass filter.
using GaussianSourceType = itk::GaussianImageSource<RealImageType>;
auto gaussianSource = GaussianSourceType::New();
gaussianSource->SetNormalized(true);
ComplexImageType::ConstPointer transformedInput = forwardFFTFilter->GetOutput();
const ComplexImageType::RegionType inputRegion(transformedInput->GetLargestPossibleRegion());
const ComplexImageType::SizeType inputSize = inputRegion.GetSize();
const ComplexImageType::SpacingType inputSpacing = transformedInput->GetSpacing();
const ComplexImageType::PointType inputOrigin = transformedInput->GetOrigin();
const ComplexImageType::DirectionType inputDirection = transformedInput->GetDirection();
gaussianSource->SetSize(inputSize);
gaussianSource->SetSpacing(inputSpacing);
gaussianSource->SetOrigin(inputOrigin);
gaussianSource->SetDirection(inputDirection);
GaussianSourceType::ArrayType sigma;
GaussianSourceType::PointType mean;
sigma.Fill(sigmaValue);
for (unsigned int ii = 0; ii < Dimension; ++ii)
{
const double halfLength = inputSize[ii] * inputSpacing[ii] / 2.0;
sigma[ii] *= halfLength;
mean[ii] = inputOrigin[ii] + halfLength;
}
mean = inputDirection * mean;
gaussianSource->SetSigma(sigma);
gaussianSource->SetMean(mean);
using FFTShiftFilterType = itk::FFTShiftImageFilter<RealImageType, RealImageType>;
auto fftShiftFilter = FFTShiftFilterType::New();
fftShiftFilter->SetInput(gaussianSource->GetOutput());
using MultiplyFilterType = itk::MultiplyImageFilter<ComplexImageType, RealImageType, ComplexImageType>;
auto multiplyFilter = MultiplyFilterType::New();
multiplyFilter->SetInput1(forwardFFTFilter->GetOutput());
multiplyFilter->SetInput2(fftShiftFilter->GetOutput());
using InverseFilterType = itk::InverseFFTImageFilter<ComplexImageType, RealImageType>;
auto inverseFFTFilter = InverseFilterType::New();
inverseFFTFilter->SetInput(multiplyFilter->GetOutput());
try
{
itk::WriteImage(inverseFFTFilter->GetOutput(), outputFileName);
}
catch (const itk::ExceptionObject & error)
{
std::cerr << "Error: " << error << std::endl;
return EXIT_FAILURE;
}
return EXIT_SUCCESS;
}
Classes demonstrated#
-
template<typename TInputImage, typename TOutputImage = Image<std::complex<typename TInputImage::PixelType>, TInputImage::ImageDimension>>
class ForwardFFTImageFilter : public itk::ImageToImageFilter<TInputImage, TOutputImage> Base class for forward Fast Fourier Transform.
This is a base class for the “forward” or “direct” discrete Fourier Transform. This is an abstract base class: the actual implementation is provided by the best child class available on the system when the object is created via the object factory system.
This class transforms a real input image into its full complex Fourier transform. The Fourier transform of a real input image has Hermitian symmetry:
 . That is, when the result of the transform is split in half along the x-dimension, the values in the second half of the transform are the complex conjugates of values in the first half reflected about the center of the image in each dimension.
. That is, when the result of the transform is split in half along the x-dimension, the values in the second half of the transform are the complex conjugates of values in the first half reflected about the center of the image in each dimension.This filter works only for real single-component input image types.
The output generated from a ForwardFFTImageFilter is in the dual space or frequency domain. Refer to FrequencyFFTLayoutImageRegionConstIteratorWithIndex for a description of the layout of frequencies generated after a forward FFT. Also see ITKImageFrequency for a set of filters requiring input images in the frequency domain.
- See
InverseFFTImageFilter, FFTComplexToComplexImageFilter
- ITK Sphinx Examples:
Subclassed by itk::FFTWForwardFFTImageFilter< TInputImage, TOutputImage >, itk::VnlForwardFFTImageFilter< TInputImage, TOutputImage >
-
template<typename TInputImage, typename TOutputImage>
class FFTShiftImageFilter : public itk::CyclicShiftImageFilter<TInputImage, TOutputImage> Shift the zero-frequency components of a Fourier transform to the center of the image.
The Fourier transform produces an image where the zero frequency components are in the corner of the image, making it difficult to understand. This filter shifts the component to the center of the image.
https://www.insight-journal.org/browse/publication/125
- Note
For images with an odd-sized dimension, applying this filter twice will not produce the same image as the original one without using SetInverse(true) on one (and only one) of the two filters.
- Author
Gaetan Lehmann. Biologie du Developpement et de la Reproduction, INRA de Jouy-en-Josas, France.
- See
ForwardFFTImageFilter, InverseFFTImageFilter
-
template<typename TInputImage1, typename TInputImage2 = TInputImage1, typename TOutputImage = TInputImage1>
class MultiplyImageFilter : public itk::BinaryGeneratorImageFilter<TInputImage1, TInputImage2, TOutputImage> Pixel-wise multiplication of two images.
This class is templated over the types of the two input images and the type of the output image. Numeric conversions (castings) are done by the C++ defaults.
- ITK Sphinx Examples:
-
template<typename TInputImage, typename TOutputImage = Image<typename TInputImage::PixelType::value_type, TInputImage::ImageDimension>>
class InverseFFTImageFilter : public itk::ImageToImageFilter<TInputImage, TOutputImage> Base class for inverse Fast Fourier Transform.
This is a base class for the “inverse” or “reverse” Discrete Fourier Transform. This is an abstract base class: the actual implementation is provided by the best child available on the system when the object is created via the object factory system.
This class transforms a full complex image with Hermitian symmetry into its real spatial domain representation. If the input does not have Hermitian symmetry, the imaginary component is discarded.
- See
ForwardFFTImageFilter, InverseFFTImageFilter
- ITK Sphinx Examples:
Subclassed by itk::FFTWInverseFFTImageFilter< TInputImage, TOutputImage >, itk::VnlInverseFFTImageFilter< TInputImage, TOutputImage >
